레이더 차트

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 플로렌스 나이팅게일과 레이더 차트
3. 구조 및 특징
- 3.1. 주요 특징
- 3.2. 한계점
4. 활용 분야
참조

1. 개요

레이더 차트는 다변량 데이터를 시각화하는 데 사용되는 그래프로, 각 데이터 변수를 축으로 표현하여 다각형 형태로 나타낸다. 플로렌스 나이팅게일이 크림 전쟁 중 전사자 및 부상자 데이터를 분석하기 위해 고안한 것으로 알려져 있으며, 데이터의 강점과 약점을 시각적으로 파악하는 데 유용하다. 스포츠 선수, 컴퓨터 프로그램, 차량, 의약품 등 다양한 분야에서 성능 비교 및 분석에 활용되며, 특히 여러 항목 간의 상대적인 비교를 통해 강점과 약점을 파악하는 데 효과적이다. 그러나 데이터의 왜곡 가능성, 시각적 비교의 어려움, 과도한 데이터 집합에서의 해석 난해함 등의 한계도 존재한다.

더 읽어볼만한 페이지

차트 - 가계도
가계도는 가족 구성원 간의 혈통 관계를 도표로 나타내며, 족보나 계통도 형태로 개인의 조상, 특정 성씨 구성원, 특정 직위 소유자 등을 포함하여 가족사 기록, 사회적 지위 표현, 문화적 전통 나타내는 데 사용되고, 최근에는 유전학적 분석을 활용하기도 한다.
차트 - 함수의 그래프
함수의 그래프는 정의역과 공역의 곱집합의 부분집합으로 정의되어 함수를 시각적으로 표현하는 방법이며, 함수의 연속성, 미분가능성 등의 성질을 파악하는 데 도움을 주지만, 모든 함수가 그래프로 표현 가능한 것은 아니다.
통계 차트와 다이어그램 - 연표
연표는 시간 순서에 따라 사건, 현상, 변화 등을 시각적으로 표현하는 방식으로, 역사 기록에서 시작하여 표 형태로 발전했으며 다양한 분야에서 활용되고 여러 형태로 정보를 제시한다.
통계 차트와 다이어그램 - 이동평균
이동 평균은 데이터 분석에서 추세 파악 및 미래 예측에 사용되는 기법으로, 단순 이동 평균, 누적 이동 평균, 가중 이동 평균, 지수 이동 평균 등 다양한 종류가 있으며, 각 종류는 고유한 장단점을 가진다.

레이더 차트
지도 정보
기본 정보
다른 이름	거미줄 차트 스타 차트 키비앗 차트 폴라 차트
유형	그래프
설명	다변량 데이터를 그래픽으로 표현하는 방법 각 변수에 대한 값을 반지름 방향으로 표시하는 축을 사용하여 여러 변수 표시 일반적으로 축은 동일한 간격으로 표시되고 값은 해당 축에 연결 각 데이터 포인트는 다각형으로 연결 축 개수와 상관없이 정적인 형태 유지 꺾은선이나 막대 그래프보다 변수 사이의 관계를 쉽게 파악 가능 여러 요소의 특성을 시각적으로 비교하는데 유용 각 변수는 서로 다른 축으로 표현 각 축은 중심점에서 시작하여 방사형으로 뻗어나감 축은 값의 범위에 따라 크기가 조정됨 각 축의 값은 데이터 포인트에 의해 표시 데이터 포인트를 연결하면 그래프의 모양 형성 이를 통해 데이터의 패턴과 추세 파악 데이터의 전반적인 특성과 변수 간의 관계를 파악 가능 다변량 데이터의 분석과 표현에 유용
역사
최초 사용	1877년 게오르크 마이어가 사용
현대적 사용	1970년대 필립 키비앗에 의해 소프트웨어 성능 측정에 사용
사용 분야
주요 사용 분야	품질 관리 성능 측정 스포츠 분석 비교 분석 시장 조사 재무 분석 환경 평가 의료 진단 소프트웨어 엔지니어링
기타 활용	여러 데이터 세트의 비교 서로 다른 변수의 중요도 시각화 다양한 개체의 특성 비교 데이터 분석 결과의 시각적 요약 개인의 강점 및 약점 분석 학생 성적 평가 웹사이트 성능 비교 에너지 소비 데이터 분석 운동 선수 성과 평가
추가 정보
장점	여러 변수를 한 번에 쉽게 비교 데이터의 패턴과 관계 시각화 여러 데이터 집합의 비교 용이 데이터의 주요 특징 식별 용이
단점	데이터가 복잡하면 그래프가 혼잡해 보일 수 있음 정확한 값 파악 어려움 변수 간의 상관관계 분석 어려움 일부 사람들에게는 이해하기 어려울 수 있음
변형	방사형 막대 그래프 별 그래프
관련 기술
연관 그래프	평행 좌표 그래프

2. 역사

레이더 차트는 데이터 값을 점으로 표시하고, 인접한 점들을 직선으로 연결하여 만든다. 연결된 선 안쪽을 색으로 채우기도 한다. 레이더 차트는 중심이 0이고, 값이 클수록 바깥쪽으로 퍼지며, 작을수록 중심에 모인다.^[25] 또한, 값들이 균형을 이룰수록 정다각형에 가까운 모양이 된다.^[25]

넓은 면적은 여러 항목에서 높은 값을 나타내므로, 종합적으로 우수하다고 볼 수 있다. 다른 항목과 비교했을 때 두드러지는 부분을 통해 강점을 파악할 수도 있다.

비슷하거나 관련 있는 속성들을 가까이 배치하면 이해하기 쉽지만, 특정 주장을 위해 단위나 측정값을 선택하면 논리적 오류를 유발할 수 있다. 각 축이 독립적인지, 어떤 의도로 결정되었는지 설명이 없으면 잘못 판단할 수 있다.^[26]

2. 1. 플로렌스 나이팅게일과 레이더 차트

플로렌스 나이팅게일이 크림 전쟁 당시 전사자 및 부상자에 대한 방대한 데이터 분석 결과를 보여주기 위해 고안했다고 여겨진다.^[27]

3. 구조 및 특징

레이더 차트는 글리프 플롯과 달리 모든 변수가 별 모양을 구성하는 데 사용된다. 전경과 배경 변수로 구분되지 않으며, 별 모양 그림은 일반적으로 페이지에 직사각형 배열로 배열된다.^[9] 관측치가 임의적이지 않은 순서로 배열될 때(변수가 의미 있는 순서로 별의 광선에 할당될 때) 데이터의 패턴을 더 쉽게 볼 수 있다.^[9]

3. 1. 주요 특징

레이더 차트는 각 변수를 나타내는 일련의 등각 방사형 선(반지름)으로 구성된 차트이자 그래프이다. 각 방사형 선의 데이터 길이는 모든 데이터 지점에 걸쳐 변수의 최대 크기에 대한 데이터 지점의 변수 크기에 비례한다. 각 방사형 선의 데이터 값을 연결하는 선이 그려진다. 이렇게 하면 플롯에 별 모양이 나타나 이러한 이름이 붙게 되었다.^[6]

별 플롯은 다음 질문에 답하는 데 사용할 수 있다.^[6]

어떤 관측치가 가장 유사한가? 즉, 관측치의 클러스터가 있는가? (레이더 차트는 단일 데이터 지점에 대한 상대적 값을 검사하고(예: 지점 3은 변수 2와 4에 대해 크고, 변수 1, 3, 5, 6에 대해 작음) 유사한 지점 또는 이질적인 지점을 찾는 데 사용된다.)^[6]
이상치가 있는가?

레이더 차트는 임의의 수의 변수를 가진 다변량 관측치를 표시하는 유용한 방법이다.^[5] 각 별은 단일 관측치를 나타낸다. 일반적으로 레이더 차트는 각 페이지에 많은 별이 있고 각 별이 하나의 관측치를 나타내는 다중 플롯 형식으로 생성된다.^[6] 별 플롯은 1877년 게오르크 폰 마이어(Georg von Mayr)가 처음 사용했다.^[7]^[8]

데이터를 플롯한 후, 인접한 데이터들을 직선으로 연결하여 작성한다. 연결된 범위를 채우는 경우도 있다.

레이더 차트는 중심이 0이며, 전체적으로 값이 클수록 바깥쪽으로 퍼지고, 전체적으로 값이 작을수록 중심에 집중된다.^[25] 또한, 균형이 잘 맞을수록 그래프의 정다각형에 가까운 형태가 된다.^[25]

높은 값을 나타내는 항목이 많을수록 즉, 면적이 넓을수록 종합적으로 우수하다고 말할 수 있다. 또한, 다른 항목과 비교하여 두드러진 부분에서 강점을 파악할 수도 있다.

유사하거나 상관관계가 있는 속성을 가까이 배치하면 이해하기 쉽다. 반대로, 특정 주장을 하기 위해 단위, 단계, 측정값 등을 선택하면 논리를 유도하게 된다. 각 축의 독립성이 있는지, 무엇을 어떤 의도로 결정했는지에 대한 설명이 없으면 판단을 잘못할 가능성이 있다.^[26]

나이팅게일이 크림 전쟁 당시 전사자 및 부상자에 대한 방대한 데이터 분석 결과를 보여주기 위해 고안했다고 여겨진다.^[27]

3. 2. 한계점

레이더 차트는 데이터에 여러 구조를 부과하는데, 이는 종종 인위적이다.

인접 변수의 관련성: 레이더 차트는 인접 변수가 관련이 없을 때 종종 사용되며, 이는 허위 연결을 만든다.^[9]
순환 구조: 첫 번째와 마지막 변수가 서로 옆에 배치된다.^[18]
길이: 변수는 종종 가장 자연스럽게 서열적이다. 즉, 더 좋거나 더 나쁘지만 차이의 정도는 인위적일 수 있다.^[9]
면적: 면적은 값의 제곱에 비례하여 확장되므로 큰 숫자의 효과를 과장한다. 예를 들어, 2, 2는 1, 1 면적의 4배를 차지한다. 이것은 면적 그래프의 일반적인 문제이며, 면적을 판단하기 어렵다.^[16]^[17]

예를 들어, 9, 1, 9, 1, 9, 1의 번갈아 가는 데이터는 스파이크 레이더 차트(안팎으로 이동)를 생성하는 반면, 데이터를 9, 9, 9, 1, 1, 1로 재정렬하면 두 개의 별개의 부채꼴(섹터)이 생성된다.

어떤 경우에는 자연스러운 구조가 있으며, 레이더 차트가 적합할 수 있다. 예를 들어, 24시간 주기 동안 변하는 데이터의 다이어그램의 경우, 시간별 데이터는 자연스럽게 이웃과 관련이 있으며 순환 구조를 가지므로 레이더 차트로 자연스럽게 표시할 수 있다.^[18]^[19]^[20]

레이더 차트는 특히 영역이 채워져 있는 경우 데이터를 어느 정도 왜곡할 수 있다. 왜냐하면 포함된 영역이 선형 측정값의 제곱에 비례하기 때문이다. 예를 들어, 1에서 100까지의 범위를 갖는 5개의 변수가 있는 차트에서 모든 측정값이 90일 때 5개의 점으로 경계 지워진 다각형이 포함하는 영역은 모든 값이 82인 차트의 영역보다 10% 이상 크다.

레이더 차트는 값이 가까워서 선이나 영역이 서로 겹쳐 보일 때, 차트의 서로 다른 표본 간에 시각적으로 비교하기 어려워질 수도 있다.

레이더 차트는 중소 규모의 다변량 데이터 집합에 유용하며, 주요 단점은 효과가 수백 개 미만의 데이터 집합으로 제한된다는 것이다. 그 이상이 되면 과도해지는 경향이 있다.^[6]

또한, 여러 차원 또는 표본을 사용하여 레이더 차트를 사용할 때, 표본 수가 증가함에 따라 레이더 차트가 어수선해지고 해석하기 어려워질 수 있다.

예를 들어, 오타니 쇼헤이의 타격 통계표를 리그 평균 지명타자와 일부 명예의 전당 선수들의 통계와 비교하는 표는 다음과 같다.

대상	타율	출루율	장타율	OPS	홈런율	삼진율	볼넷율
MLB	0.244	0.317	0.411	0.728	0.037	0.232	0.087
지명타자	0.239	0.316	0.434	0.75	0.047	0.256	0.093
오타니 쇼헤이	0.257	0.372	0.592	0.965	0.086	0.296	0.15
재키 로빈슨	0.313	0.41	0.477	0.887	0.0282	0.0582	0.151
짐 토미	0.276	0.402	0.554	0.956	0.072	0.302	0.207
프랭크 토머스	0.301	0.419	0.555	0.974	0.063	0.17	0.203

레이더 차트는 축과 표본의 수가 상대적으로 적을 때 쉽게 해석될 수 있지만, 더 많은 표본을 비교할 때, 레이더 차트에 면적 채우기를 사용하지 않더라도 해석하거나 절충안을 결정하기가 어려워질 수 있다.

방사형 거리를 판단하기 어렵기 때문에 서로 다른 스포크의 길이를 시각적으로 비교하기 어렵지만, 동심원이 눈금선으로 도움이 된다. 특히 시계열의 경우 간단한 선 그래프를 사용할 수 있다.^[18]

유사하거나 상관관계가 있는 속성을 가까이 배치하면 이해하기 쉽지만, 특정 주장을 하기 위해 단위, 단계, 측정값 등을 선택하면 논리를 유도하게 된다. 각 축의 독립성이 있는지, 무엇을 어떤 의도로 결정했는지에 대한 설명이 없으면 판단을 잘못할 가능성이 있다.^[26]

4. 활용 분야

레이더 차트는 스포츠, 의료, 성능 평가 등 다양한 분야에서 활용된다.^[12]

스포츠: 선수들의 강점과 약점을 파악하고 훈련 방식을 개선하는 데 활용된다. 예를 들어, 농구 선수의 슛 성공률, 리바운드, 어시스트 등을 레이더 차트로 나타내어 다른 선수나 리그 평균과 비교할 수 있다.
의료: 약물의 효과와 부작용을 비교하거나 환자의 건강 상태를 분석하는 데 사용된다. 예를 들어, 두 가지 항우울제의 효능, 부작용, 비용 등을 레이더 차트로 나타내어 비교할 수 있다.
성능 평가: 컴퓨터 프로그램, 자동차 등 다양한 제품의 성능 지표를 비교하고 품질 개선을 관리하는 데 활용된다. 예를 들어, 여러 정렬 알고리즘의 속도, 메모리 사용량, 전력 사용량을 레이더 차트로 나타내어 비교할 수 있다.

4. 1. 스포츠

레이더 차트는 선수의 강점과 약점을 나타내는 데 사용될 수 있다.^[10] 차트 중심축을 따라 추적할 수 있는 선수 관련 다양한 통계를 계산하여 이를 표현한다. 예를 들어 농구 선수의 슛 성공률, 리바운드, 어시스트 등이나 야구 선수의 타격 또는 투구 통계 등이 있다. 이를 통해 선수의 강점과 약점을 중앙 집중식으로 시각화하고, 다른 선수의 통계 또는 리그 평균과 겹쳐 표시하면 선수가 어떤 부분에서 뛰어나고 어떤 부분을 개선해야 하는지 알 수 있다.^[11]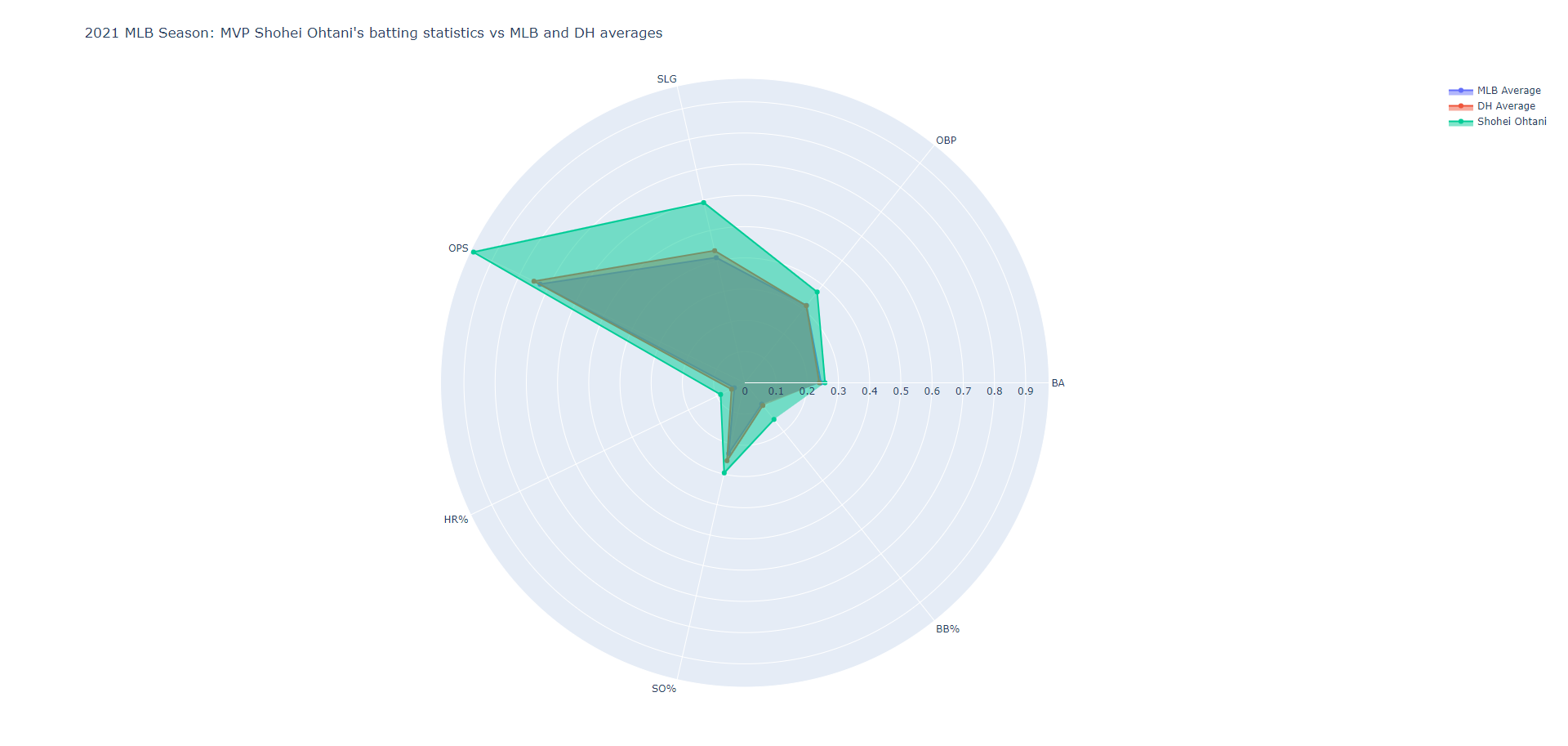

2021년 MLB 시즌 타격 통계를 보여주는 레이더 차트. 녹색으로 표시된 오타니 쇼헤이는 같은 시즌 지명타자(DH) 평균(빨간색)과 MLB 평균(파란색)을 능가하지만, 삼진율도 더 높다.

이러한 선수의 강점과 약점에 대한 통찰력은 코치와 트레이너가 선수의 훈련 방식을 조정하여 약점을 개선하는 데 도움이 되므로 선수 육성에 매우 중요할 수 있다. 레이더 차트의 결과는 상황별 플레이에도 유용하게 활용될 수 있다. 예를 들어 좌완 투수를 상대로 타격이 좋지 않은 타자라면, 팀은 좌완 투수를 상대로 타석에 들어서는 횟수를 제한하는 반면, 상대 팀은 그 타자를 좌완 투수와 대결하게 만들려고 할 수 있다.

4. 2. 의료

레이더 차트는 생명 과학에서 약물 및 기타 의약품의 강점과 약점을 표시하는 데 사용될 수 있다.^[13] 예를 들어, 두 가지 항우울제를 비교할 때, 연구자는 효능, 부작용, 비용 등의 변수를 1점에서 10점 척도로 평가할 수 있다. 그런 다음 레이더 차트를 사용하여 결과를 그래프로 표시하여 변수의 분포를 확인할 수 있다. 이를 통해 한 항우울제는 저렴하고 작용이 빠르지만 시간이 지남에 따라 효과가 크지 않은 반면, 다른 항우울제는 효과가 더 크고 시간이 지나도 효과가 지속되지만 더 비싸다는 차이점을 쉽게 파악할 수 있다.

또 다른 생명 과학 응용 분야는 환자 분석이다. 레이더 차트를 사용하여 사람의 건강에 영향을 미치는 변수를 그래프로 표시하고 분석하여 환자를 도울 수 있다.^[14] 예를 들어, 운동선수의 경우 수면, 식단, 스트레스와 같은 다양한 건강 습관을 모니터링하여 최상의 신체 상태를 유지하도록 할 수 있다. 어떤 영역이 저하되는 것으로 나타나면 의사와 트레이너가 선수를 돕고 건강을 개선하기 위해 개입할 수 있다.

4. 3. 성능 평가

레이더 차트는 컴퓨터 프로그램,^[12] 컴퓨터, 휴대전화, 차량 등 다양한 객체의 성능 지표를 표시하여 품질 개선을 관리하는 데 사용된다. 예를 들어, 여러 정렬 알고리즘의 성능을 분석할 때 레이더 차트를 사용하여 각 알고리즘의 속도, 메모리 사용량, 전력 사용량을 비교할 수 있다. 소비자는 자동차의 최고 속도, 연비, 마력, 토크와 같은 변수를 레이더 차트로 시각화하여 자신에게 가장 적합한 자동차를 결정할 수 있다.

레이더 차트는 주로 눈에 띄는 이상치와 공통성을 보여주는 데 적합하며, 한 차트가 다른 차트보다 모든 변수에서 더 큰 경우, 그리고 주로 서열 측정에 사용된다. 즉, 각 변수가 어떤 면에서 "더 좋다"에 해당하고 모든 변수가 같은 척도에 있을 때 유용하다.

반면, 레이더 차트는 한 차트가 다른 차트보다 일부 변수에서는 더 크지만 다른 변수에서는 더 작은 경우, 즉 절충 결정을 내리는 데 적합하지 않다는 비판을 받아왔다.^[15] 또한, 방사형 거리를 판단하기 어렵기 때문에 서로 다른 스포크(spoke)의 길이를 시각적으로 비교하기 어렵지만, 동심원이 눈금선으로 도움이 된다.^[18]

레이더 차트는 특히 영역이 채워져 있는 경우 데이터를 어느 정도 왜곡할 수 있다. 왜냐하면 포함된 영역이 선형 측정값의 제곱에 비례하기 때문이다. 예를 들어, 1에서 100까지의 범위를 갖는 5개의 변수가 있는 차트에서 모든 측정값이 90일 때, 5개의 점으로 경계 지워진 다각형이 포함하는 영역은 모든 값이 82인 차트의 영역보다 10% 이상 크다.

레이더 차트는 값이 가까워서 선이나 영역이 서로 겹쳐 보일 때 차트의 서로 다른 표본 간에 시각적으로 비교하기 어려워질 수 있다.

레이더 차트는 중소 규모의 다변량 데이터 집합에 유용하며, 수백 개 미만의 데이터 집합에 효과적이다. 그 이상이 되면 과도해지는 경향이 있다.^[6] 또한, 여러 차원 또는 표본을 사용하여 레이더 차트를 사용할 때, 표본 수가 증가함에 따라 레이더 차트가 어수선해지고 해석하기 어려워질 수 있다.

예를 들어, MLB 2021 MVP 오타니 쇼헤이(Shohei Ohtani)의 타격 통계를 리그 평균 지명타자와 명예의 전당 선수들의 통계와 비교하는 표를 보자.

대상	타율	출루율	장타율	OPS	홈런율	삼진율	볼넷율
MLB	0.244	0.317	0.411	0.728	0.037	0.232	0.087
지명타자	0.239	0.316	0.434	0.75	0.047	0.256	0.093
오타니 쇼헤이(Shohei Ohtani)	0.257	0.372	0.592	0.965	0.086	0.296	0.15
재키 로빈슨(Jackie Robinson)	0.313	0.41	0.477	0.887	0.0282	0.0582	0.151
짐 토미(Jim Thome)	0.276	0.402	0.554	0.956	0.072	0.302	0.207
프랭크 토마스(Frank Thomas)	0.301	0.419	0.555	0.974	0.063	0.17	0.203

위 표를 바탕으로 레이더 차트를 만들면, 축과 표본의 수가 적을 때는 해석이 쉽지만, 표본이 많아지면 해석이 어려워지는 것을 알 수 있다.

4. 4. 기타

레이더 차트는 여러 종류의 변수를 가진 다변량 관측치를 표시하는 유용한 방법이다.^[5] 각 별 모양은 단일 관측치를 나타내며, 일반적으로 각 페이지에 많은 별이 있고 각 별이 하나의 관측치를 나타내는 다중 플롯 형식으로 생성된다.^[6] 레이더 차트는 1877년 게오르크 폰 마이어(Georg von Mayr)가 처음 사용했다.^[7]^[8]

레이더 차트는 모든 변수가 별 모양을 구성하는 데 사용된다는 점에서 글리프 플롯과 다르다. 전경과 배경 변수로 구분되지 않으며, 별 모양 그림은 일반적으로 페이지에 직사각형 배열로 배열된다.^[9]

레이더 차트는 주로 눈에 띄는 이상치와 공통성을 보여주는 데 적합하며, 한 차트가 다른 차트보다 모든 변수에서 더 큰 경우, 그리고 주로 서열 측정에 사용된다. 즉, 각 변수가 어떤 면에서 "더 좋다"에 해당하고 모든 변수가 같은 척도에 있을 때 유용하다.

반면, 레이더 차트는 한 차트가 다른 차트보다 일부 변수에서는 더 크지만 다른 변수에서는 더 작은 경우, 즉 절충 결정을 내리는 데 적합하지 않다는 비판을 받아왔다.^[15] 또한, 방사형 거리를 판단하기 어렵기 때문에 서로 다른 스포크(spoke)의 길이를 시각적으로 비교하기 어렵지만, 동심원이 눈금선으로 도움이 된다. 이 때문에 시계열 데이터와 같은 경우에는 간단한 선 그래프를 대신 사용할 수 있다.^[18]

레이더 차트는 특히 영역이 채워져 있는 경우 데이터를 왜곡할 수 있다. 포함된 영역이 선형 측정값의 제곱에 비례하기 때문이다. 예를 들어, 1에서 100까지의 범위를 갖는 5개 변수가 있는 차트에서 모든 측정값이 90일 때, 5개 점으로 경계 지워진 다각형이 포함하는 영역은 모든 값이 82인 차트의 영역보다 10% 이상 크다. 또한, 값이 가까워서 선이나 영역이 서로 겹쳐 보일 때 차트의 서로 다른 표본 간에 시각적으로 비교하기 어려워질 수 있다.

레이더 차트는 다음과 같이 종종 인위적인 데이터 구조를 부과한다.

인접 변수의 관련성: 인접 변수가 관련이 없을 때 레이더 차트가 종종 사용되어 허위 연결을 만들 수 있다.
순환 구조: 첫 번째와 마지막 변수가 서로 옆에 배치된다.
길이: 변수는 종종 서열적(더 좋거나 나쁨)이지만, 차이의 정도는 인위적일 수 있다.
면적: 면적은 값의 제곱에 비례하여 확장되므로 큰 숫자의 효과를 과장한다. (예: 2, 2는 1, 1 면적의 4배) 이는 면적 그래프의 일반적인 문제이며, 면적을 판단하기 어렵다. ("클리블랜드의 계층 구조" 참조)^[16]^[17]

예를 들어, 9, 1, 9, 1, 9, 1의 번갈아 가는 데이터는 스파이크 레이더 차트(안팎으로 이동)를 생성하는 반면, 데이터를 9, 9, 9, 1, 1, 1로 재정렬하면 두 개의 별개 부채꼴(섹터)이 생성된다.

하지만 24시간 주기 동안 변하는 데이터와 같이 자연스러운 구조가 있는 경우에는 레이더 차트가 적합할 수 있다. 시간별 데이터는 자연스럽게 이웃과 관련이 있으며 순환 구조를 가지므로 레이더 차트로 자연스럽게 표시할 수 있다.^[18]^[19]^[20]

레이더 차트 사용 지침은 다음과 같다.^[20]

공통 눈금을 따라 위치 대신 누적된 영역을 읽는 것을 신경 쓰지 않는다(클리블랜드의 계층 구조 참조).
데이터 세트가 선형이 아닌 순환적이다.
비교할 두 계열이 있으며, 그중 하나가 다른 하나보다 훨씬 작다.

여러 변수를 가진 2차원 표 형태 데이터의 질적 비교를 위한 그래픽으로는 컨슈머 리포트(Consumer Reports)에서 광범위하게 사용되는 하비 볼(Harvey balls)이 일반적인 대안이다.^[22] 하비 볼(및 레이더 차트)에서의 비교는 변수를 알고리즘적으로 정렬하여 순서를 추가함으로써 상당히 향상될 수 있다.^[23]

다변량 데이터 내 구조를 시각화하는 훌륭한 방법으로는 주성분 분석(principal component analysis, PCA)이 있다. 또 다른 대안으로는 작은 인라인 막대 차트를 사용하는 방법이 있으며, 이는 스파크라인(sparkline)과 비교될 수 있다.^[23]

레이더 차트와 극좌표 차트는 종종 동일한 차트 유형으로 설명되지만,^[4] 일부 자료에서는 이 둘을 구분하고, 레이더 차트를 극좌표 좌표계로 데이터를 표시하지 않는 극좌표 차트의 변형으로 간주하기도 한다.^[24] 데이터를 플롯한 후, 인접한 데이터들을 직선으로 연결하며, 연결된 범위를 채우는 경우도 있다.

레이더 차트는 중심이 0이며, 전체적으로 값이 클수록 바깥쪽으로 퍼지고, 작을수록 중심에 집중된다.^[25] 또한, 균형이 잘 맞을수록 그래프는 정다각형에 가까운 형태가 된다.^[25]

높은 값을 나타내는 항목이 많을수록, 즉 면적이 넓을수록 종합적으로 우수하다고 말할 수 있다. 또한, 다른 항목과 비교하여 두드러진 부분에서 강점을 파악할 수도 있다. 유사하거나 상관관계가 있는 속성을 가까이 배치하면 이해하기 쉽지만, 특정 주장을 하기 위해 단위, 단계, 측정값 등을 선택하면 논리를 유도하게 된다. 따라서 각 축의 독립성이 있는지, 무엇을 어떤 의도로 결정했는지에 대한 설명이 없으면 판단을 잘못할 가능성이 있다.^[26]

나이팅게일이 크림 전쟁 당시 전사자 및 부상자에 대한 방대한 데이터 분석 결과를 보여주기 위해 고안했다고 여겨진다.^[27]

참조

_[1] 논문 Multidimensional mechanics: Performance mapping of natural biological systems using permutated radar charts 2018
_[2] 서적 The quality toolbox 2005
_[3] 논문 The Software Empiricist 1973
_[4] 웹사이트 Find Content Gaps Using Radar Charts http://www.content-w[...] Content Strategy Workshops 2015-03-03
_[5] 서적 Graphical Methods for Data Analysis Wadsworth 1983
_[6] 웹사이트 Star Plot http://www.itl.nist.[...] NIST/SEMATECH 2003-06-01
_[7] 서적 Die Gesetzmäßigkeit im Gesellschaftsleben Oldenbourg
_[8] 웹사이트 Milestones in the history of thematic cartography, statistical graphics, and data visualization http://www.math.york[...] 2008
_[9] 웹사이트 Statistical Graphics for Multivariate Data http://www.math.york[...] 1991-04
_[10] 웹사이트 Spider Graphs: Charting Basketball Statistics http://howtowatchspo[...]
_[11] 웹사이트 Making sense of data visualizations http://seeingdata.or[...] Seeing Data
_[12] 서적 Implementing Quality: A Practical Guide to Tools and Techniques 2004
_[13] 웹사이트 Effective Use of Radar Charts https://msktc.org/li[...] Model Systems Knowledge Translation Center
_[14] 웹사이트 De-normalized Spider and Radar Graphs https://www.kitmanla[...] Kitman Labs
_[15] 웹사이트 You are NOT spider man, so why do you use radar charts? http://chandoo.org/w[...] 2008-09-18
_[16] 논문 Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods https://web.archive.[...] 1984
_[17] 논문 Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods https://web.archive.[...] 1984
_[18] 웹사이트 Rock Around The Clock - Peltier Tech Blog http://peltiertech.c[...] Peltiertech.com 2008-08-14
_[19] 웹사이트 Charting around the clock The Excel Charts Blog http://www.excelchar[...] Excelcharts.com 2008-08-15
_[20] 웹사이트 Clock This http://i-ocean.blogs[...]
_[21] 웹사이트 Standard Stats https://www.mlb.com/[...]
_[22] 웹사이트 Qualitative Comparison http://supportanalyt[...] Support Analytics Blog 2007-12-11
_[23] 웹사이트 Information Ocean: Reorderable tables II: Bertin versus the Spiders http://i-ocean.blogs[...] I-ocean.blogspot.com 2008-09-24
_[24] 웹사이트 Polar Charts (Report Builder and SSRS) https://msdn.microso[...] Microsoft Developer Network
_[25] 뉴스 レーダーチャート : 総務省統計局 https://www.stat.go.[...]
_[26] 서적 数学チュートリアル　やさしく語る確率統計オーム社
_[27] 웹사이트 ナイチンゲールと統計総務省統計局 https://www.stat.go.[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com